Home>Education & Research>Understanding The Arrhenius Equation: Definition, Formula, And Applications
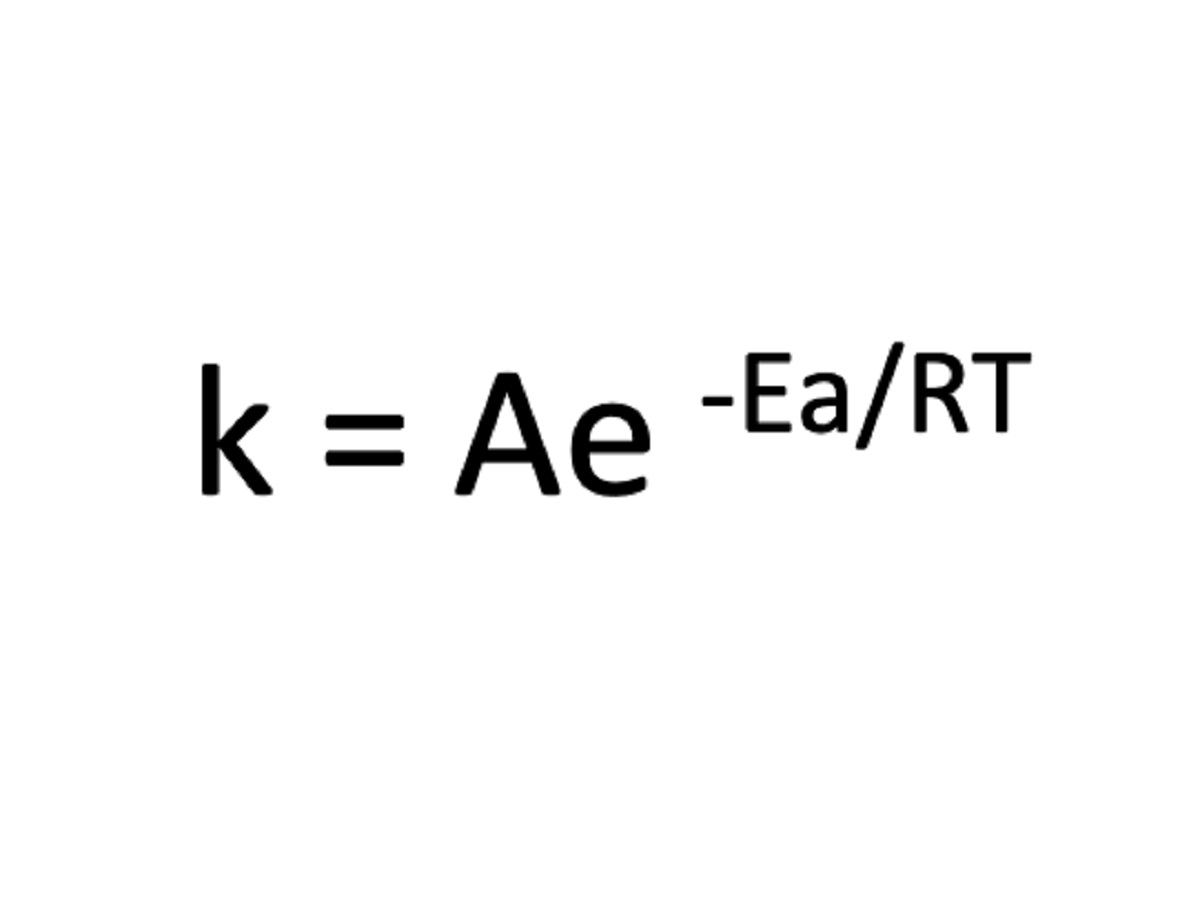
Education & Research
Understanding The Arrhenius Equation: Definition, Formula, And Applications
Published: February 19, 2024
Learn about the Arrhenius Equation, its formula, and practical applications in education and research. Understand the significance of this fundamental concept.
(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Temperatures.com, at no extra cost. Learn more)
Table of Contents
Introduction
The Arrhenius Equation is a fundamental concept in chemistry and chemical kinetics, providing a quantitative understanding of the relationship between temperature and the rate of chemical reactions. Named after the Swedish scientist Svante Arrhenius, who first proposed it in 1889, the equation has since become a cornerstone in the study of reaction kinetics and has found widespread applications in various scientific and industrial fields.
Understanding the factors that influence the rate of chemical reactions is crucial for predicting and controlling the behavior of chemical systems. The Arrhenius Equation plays a pivotal role in this understanding by elucidating the impact of temperature on reaction rates. As such, it serves as a powerful tool for researchers, engineers, and scientists seeking to optimize reaction conditions, develop new materials, and improve industrial processes.
In this article, we will delve into the intricacies of the Arrhenius Equation, exploring its derivation, formula, and applications. We will also examine the concept of activation energy, which forms the basis of the equation, and discuss the factors that influence the rate constant. Furthermore, we will explore real-world applications of the Arrhenius Equation, shedding light on its significance in diverse fields such as chemical engineering, environmental science, and materials science.
By gaining a comprehensive understanding of the Arrhenius Equation, readers will be equipped with valuable insights into the temperature dependence of chemical reactions and the practical implications of this fundamental relationship. Through this exploration, we aim to demystify the complexities of reaction kinetics and highlight the profound impact of the Arrhenius Equation on scientific research and technological advancements.
The Concept of Activation Energy
In the realm of chemical kinetics, the concept of activation energy stands as a critical determinant of reaction rates. Activation energy, often denoted as Ea, represents the minimum amount of energy required for a chemical reaction to occur. Visualize it as a barrier that must be surmounted for the transformation of reactants into products to take place. This energy barrier arises from the need to destabilize existing chemical bonds in the reactant molecules before new bonds can form, a process that demands a certain level of energy input.
The significance of activation energy becomes apparent when considering the collision theory of chemical reactions. According to this theory, for a reaction to proceed, reactant molecules must collide with sufficient energy and in the correct orientation. Only collisions that possess energy equal to or greater than the activation energy lead to successful chemical transformations. Consequently, the magnitude of the activation energy profoundly influences the reaction rate, as it dictates the likelihood of productive collisions occurring within a given timeframe.
Moreover, activation energy reflects the inherent stability of the reactant molecules. Substances with higher activation energies typically exhibit greater stability, as they necessitate more energy to initiate the breaking of chemical bonds and initiate the reaction process. Conversely, compounds with lower activation energies are more prone to undergoing chemical transformations, as they require relatively less energy to surmount the energy barrier.
Understanding the concept of activation energy is pivotal for elucidating the temperature dependence of reaction rates, a relationship that forms the crux of the Arrhenius Equation. As temperature increases, the distribution of molecular energies broadens, leading to a greater proportion of molecules surpassing the activation energy threshold. Consequently, higher temperatures result in elevated reaction rates, a phenomenon encapsulated by the exponential temperature dependence described by the Arrhenius Equation.
In essence, activation energy serves as a fundamental parameter in characterizing the kinetics of chemical reactions, offering profound insights into the energy requirements and molecular dynamics underlying the transformation of reactants into products. By comprehending the role of activation energy, researchers and scientists can manipulate reaction conditions, design catalysts, and engineer materials with tailored properties, thereby harnessing the principles of chemical kinetics to drive innovation and progress across diverse scientific domains.
The Arrhenius Equation: Derivation and Formula
The Arrhenius Equation, formulated by Svante Arrhenius in 1889, stands as a cornerstone in the realm of chemical kinetics, offering a quantitative framework for understanding the temperature dependence of reaction rates. At its core, the equation provides a mathematical expression that relates the rate constant of a chemical reaction to the temperature at which the reaction occurs. By elucidating this fundamental relationship, the Arrhenius Equation empowers scientists and researchers to unravel the intricate interplay between temperature and reaction kinetics, thereby unlocking valuable insights into the behavior of chemical systems.
The derivation of the Arrhenius Equation stems from a profound understanding of the collision theory of chemical reactions and the concept of activation energy. According to the collision theory, for a chemical reaction to occur, reactant molecules must collide with sufficient energy and in the correct orientation. This concept aligns with the notion of activation energy, which represents the minimum energy required for a reaction to proceed. Building upon these foundational principles, Arrhenius postulated that the rate constant (k) of a reaction is exponentially dependent on the temperature (T), as encapsulated by the following equation:
[ k = A cdot e^{-frac{E_a}{RT}} ]
In this equation, 'k' denotes the rate constant, 'A' represents the pre-exponential factor or frequency factor, 'Ea' signifies the activation energy, 'R' denotes the universal gas constant, and 'T' stands for the absolute temperature. The exponential term, (-frac{E_a}{RT}), embodies the temperature dependence of the rate constant, reflecting the impact of temperature on the likelihood of successful collisions and the subsequent progression of the reaction.
The Arrhenius Equation offers a compelling insight into the temperature sensitivity of chemical reactions, highlighting the exponential relationship between temperature and reaction rates. As temperature rises, the exponential term in the equation amplifies, leading to a corresponding increase in the rate constant and, consequently, the reaction rate. This temperature-dependent behavior underscores the pivotal role of thermal energy in driving chemical transformations and underscores the profound influence of temperature on the kinetics of diverse chemical processes.
By encapsulating the intricate interplay between temperature, activation energy, and reaction rates, the Arrhenius Equation provides a robust framework for predicting and manipulating the kinetics of chemical reactions. Its widespread applicability across scientific disciplines and industrial sectors underscores its significance as a foundational principle in the study of reaction kinetics, catalysis, and materials science. Through the elegant simplicity of its formula, the Arrhenius Equation continues to inspire groundbreaking research and technological innovations, cementing its status as a timeless cornerstone in the realm of chemical kinetics.
Factors Affecting the Rate Constant
The rate constant, denoted as 'k' in the Arrhenius Equation, serves as a pivotal parameter that encapsulates the intrinsic propensity of a chemical reaction to progress. Numerous factors intricately influence the magnitude of the rate constant, thereby exerting profound impacts on the kinetics and dynamics of chemical transformations. By comprehending the diverse determinants that govern the rate constant, researchers and scientists can gain valuable insights into the underlying mechanisms of chemical reactions and tailor reaction conditions to achieve desired outcomes.
Temperature:
Temperature stands as a paramount factor influencing the rate constant of a chemical reaction. As elucidated by the Arrhenius Equation, the exponential temperature dependence of the rate constant underscores the profound impact of thermal energy on reaction kinetics. Elevated temperatures broaden the distribution of molecular energies, leading to a greater proportion of molecules surpassing the activation energy barrier. Consequently, higher temperatures result in heightened reaction rates, as reflected by the exponential temperature term in the Arrhenius Equation. This temperature sensitivity underscores the fundamental role of thermal energy in driving chemical transformations and underscores the significance of temperature control in modulating reaction kinetics.
Activation Energy:
The magnitude of the activation energy (Ea) profoundly influences the rate constant, serving as a critical threshold that dictates the likelihood of successful collisions and subsequent reaction progression. Chemical reactions characterized by higher activation energies necessitate greater energy inputs for the initiation of the reaction process, resulting in lower rate constants at a given temperature. Conversely, reactions with lower activation energies exhibit higher rate constants, as they require relatively less energy for the transformation of reactants into products. Understanding the interplay between activation energy and the rate constant is pivotal for predicting and manipulating the kinetics of chemical reactions, offering valuable insights into the energy requirements and molecular dynamics underlying chemical transformations.
Catalysts:
The presence of catalysts represents a pivotal factor that can significantly alter the rate constant of a chemical reaction. Catalysts function by providing alternative reaction pathways with lower activation energies, thereby facilitating the transformation of reactants into products. By lowering the activation energy barrier, catalysts effectively enhance the rate constant, leading to accelerated reaction rates without undergoing permanent chemical changes themselves. The profound influence of catalysts on the rate constant underscores their pivotal role in industrial processes, where they are employed to optimize reaction conditions, improve efficiency, and minimize energy consumption.
Molecular Orientation and Collision Frequency:
The relative orientation of colliding molecules and the frequency of successful collisions represent additional factors that impact the rate constant. For a chemical reaction to occur, reactant molecules must collide with sufficient energy and in the correct orientation. Variations in molecular orientation and collision frequency can influence the likelihood of productive collisions, thereby affecting the rate constant. Factors such as molecular shape, steric hindrance, and intermolecular forces play crucial roles in governing the collision dynamics and, consequently, the rate constant of chemical reactions.
By comprehensively examining the diverse factors that influence the rate constant, researchers and scientists can gain a nuanced understanding of the intricate interplay between reaction kinetics and the underlying molecular dynamics. This multifaceted comprehension empowers the manipulation of reaction conditions, the design of efficient catalysts, and the optimization of industrial processes, thereby driving innovation and progress across diverse scientific domains.
Applications of the Arrhenius Equation
The applications of the Arrhenius Equation span a diverse array of scientific disciplines and industrial sectors, underscoring its profound significance in elucidating the temperature dependence of chemical reactions and guiding the optimization of reaction conditions. By harnessing the insights offered by the Arrhenius Equation, researchers and engineers have unlocked a myriad of applications that have catalyzed advancements in fields ranging from chemical engineering to environmental science and materials research.
Read more: Why Are the Poles Colder Than the Equator?
Chemical Engineering and Industrial Processes
In the realm of chemical engineering, the Arrhenius Equation serves as a fundamental tool for optimizing reaction conditions and designing efficient chemical processes. By quantifying the temperature dependence of reaction rates, engineers can precisely tailor reaction conditions to maximize efficiency, minimize energy consumption, and enhance product yields. Furthermore, the equation facilitates the selection and design of catalysts, enabling the development of novel catalytic systems that drive industrial processes with heightened efficacy and sustainability. From petrochemical refineries to pharmaceutical manufacturing, the Arrhenius Equation underpins the optimization of reaction kinetics, thereby fostering innovation and progress in chemical engineering and industrial sectors.
Environmental Science and Atmospheric Chemistry
The Arrhenius Equation finds compelling applications in the realm of environmental science, particularly in the study of atmospheric chemistry and pollutant degradation. By elucidating the temperature dependence of reaction rates, the equation enables scientists to model and predict the behavior of atmospheric pollutants, such as ozone-depleting substances and greenhouse gases. This understanding is pivotal for assessing the impact of human activities on the environment and formulating strategies to mitigate pollution. Moreover, the Arrhenius Equation guides the development of kinetic models that underpin atmospheric chemistry simulations, offering valuable insights into the complex interplay between temperature, chemical reactions, and environmental processes.
Materials Science and Kinetic Studies
In the domain of materials science, the Arrhenius Equation serves as a cornerstone for elucidating the kinetics of diverse processes, including phase transformations, diffusion phenomena, and solid-state reactions. By quantifying the temperature dependence of reaction rates, the equation facilitates the design and engineering of materials with tailored properties, offering insights into processes such as sintering, crystallization, and thermal degradation. Moreover, the Arrhenius Equation guides kinetic studies that underpin the development of advanced materials, ranging from high-performance alloys to functional ceramics, thereby driving innovation in materials science and engineering.
Pharmaceutical and Biomedical Research
In the realm of pharmaceutical and biomedical research, the Arrhenius Equation finds applications in elucidating the stability and degradation kinetics of drugs, biomolecules, and pharmaceutical formulations. By quantifying the temperature dependence of degradation reactions, the equation guides the formulation of storage conditions and shelf-life predictions for pharmaceutical products, ensuring their efficacy and safety. Furthermore, the Arrhenius Equation underpins the design of accelerated stability studies that facilitate the rapid assessment of drug stability under diverse temperature conditions, thereby expediting the development and commercialization of pharmaceutical formulations.
In essence, the Arrhenius Equation stands as a versatile and indispensable tool that permeates diverse scientific disciplines and industrial domains, offering profound insights into the temperature dependence of chemical reactions and guiding the optimization of reaction conditions. Its applications underscore its enduring significance as a foundational principle in the study of reaction kinetics, catalysis, and materials science, driving innovation and progress across multifaceted scientific and technological frontiers.
Limitations and Criticisms of the Arrhenius Equation
While the Arrhenius Equation has significantly contributed to our understanding of reaction kinetics and temperature-dependent rate constants, it is essential to acknowledge its limitations and the criticisms it has garnered over time. By critically examining these aspects, we can gain a nuanced perspective on the practical constraints and theoretical considerations associated with the application of the Arrhenius Equation.
Complex Reaction Mechanisms:
One of the primary limitations of the Arrhenius Equation arises from its assumption of a simple, unimolecular reaction mechanism. In reality, many chemical reactions involve intricate multi-step processes, intermediate species, and complex reaction pathways. The Arrhenius Equation's reliance on a single activation energy value does not adequately capture the nuanced intricacies of such complex reactions, leading to deviations between predicted and observed reaction rates.
Temperature Range Dependence:
Another criticism pertains to the temperature range over which the Arrhenius Equation remains valid. While the equation effectively describes the temperature dependence of reaction rates within a certain range, it may falter at extreme temperatures or under conditions where non-Arrhenius behavior is exhibited. At very high temperatures, for instance, deviations from the exponential temperature dependence may occur due to thermal decomposition, radical reactions, or other non-Arrhenius phenomena, challenging the equation's applicability in such regimes.
Pressure and Solvent Effects:
The Arrhenius Equation's focus on temperature as the sole variable overlooks the potential influence of pressure and solvent effects on reaction kinetics. In reality, variations in pressure and the nature of the solvent can significantly impact reaction rates, leading to deviations from the predictions offered by the Arrhenius Equation. This limitation underscores the need for more comprehensive kinetic models that account for the multifaceted interplay between temperature, pressure, and solvent effects in governing reaction kinetics.
Read more: Understanding The Climate Of Mars
Quantum Mechanical Considerations:
From a theoretical standpoint, the Arrhenius Equation's classical treatment of reaction kinetics neglects quantum mechanical effects that may influence the energy landscape of chemical reactions. Quantum tunneling, zero-point energy, and other quantum phenomena can play pivotal roles in certain reactions, particularly those involving light atoms or highly strained molecular configurations. The equation's classical framework may thus overlook quantum mechanical contributions to reaction rates, necessitating a more nuanced theoretical treatment.
Deviations in Pre-Exponential Factor:
The pre-exponential factor (A) in the Arrhenius Equation, often referred to as the frequency factor, represents the collision frequency and orientation factor of reactant molecules. However, accurately determining this factor for complex reactions or heterogeneous systems can pose significant challenges. Deviations in the estimated pre-exponential factor can lead to discrepancies between predicted and observed reaction rates, highlighting the limitations in quantifying this crucial parameter.
By acknowledging these limitations and criticisms, we recognize the need for more sophisticated kinetic models that transcend the constraints of the Arrhenius Equation. While the equation remains a valuable tool for understanding the temperature dependence of reaction rates, addressing these limitations is pivotal for advancing our comprehension of complex reaction kinetics and developing more robust predictive frameworks.
Conclusion
In conclusion, the Arrhenius Equation stands as a timeless cornerstone in the realm of chemical kinetics, offering profound insights into the temperature dependence of reaction rates and guiding the optimization of reaction conditions across diverse scientific disciplines and industrial sectors. By encapsulating the exponential relationship between temperature and the rate constant, the equation has empowered researchers, engineers, and scientists to unravel the intricate interplay between thermal energy and chemical transformations, driving innovation and progress in fields ranging from chemical engineering to environmental science and materials research.
The concept of activation energy, fundamental to the Arrhenius Equation, serves as a pivotal parameter in characterizing the kinetics of chemical reactions, offering profound insights into the energy requirements and molecular dynamics underlying the transformation of reactants into products. By comprehending the role of activation energy, researchers and scientists can manipulate reaction conditions, design catalysts, and engineer materials with tailored properties, thereby harnessing the principles of chemical kinetics to drive innovation and progress across diverse scientific domains.
Furthermore, the applications of the Arrhenius Equation permeate multifaceted scientific disciplines and industrial domains, underscoring its enduring significance as a foundational principle in the study of reaction kinetics, catalysis, and materials science. From optimizing industrial processes in chemical engineering to elucidating the stability of pharmaceutical formulations, the equation has catalyzed advancements that have profound implications for human health, environmental sustainability, and technological innovation.
However, it is crucial to acknowledge the limitations and criticisms of the Arrhenius Equation, particularly concerning its applicability to complex reaction mechanisms, temperature range dependence, pressure and solvent effects, quantum mechanical considerations, and the quantification of the pre-exponential factor. Addressing these constraints is pivotal for advancing our comprehension of complex reaction kinetics and developing more robust predictive frameworks that transcend the limitations of the classical Arrhenius framework.
In essence, the Arrhenius Equation continues to inspire groundbreaking research and technological innovations, cementing its status as a versatile and indispensable tool that drives innovation and progress across multifaceted scientific and technological frontiers. Its enduring legacy as a fundamental principle in chemical kinetics underscores its profound impact on scientific research, industrial processes, and technological advancements, shaping the trajectory of innovation and progress in the realms of chemistry, materials science, and beyond.











